cs231n: Summary

Neural Networks

Image Classification: Data-driven Approach, k-Nearest Neighbor, train/val/test splits

Image Classification

Using a set of labeled images to predict categories of a set of test images. Then we can measure the accuracy of the predictions.

Nearest Neighbor classifier

Choose a distance(L1, L2, etc.)
Calculate the sum of the distance between each text data and all the train data. Get the closest one. The label of this data is what the classifier predict.

kNN classifier

Find the top k closest images and then have them vote on the label of the test image.

Validation set, cross-validation

In this picture, fold 5 is the validation set. For cross-validation, we let fold 1-5 be validation set separately to help us choose some hyperparameters.

Linear classification: Support Vector Machine, Softmax

What we want: a map from images to label scores. \(\Rightarrow\) Score function, Loss function

Score function

\(x_i\) is a picture and \(W\) is a matrix named weights. And \(b\) is bias.
\[ f(x_i,W,b)=Wx_i+b \] Sometimes we can extend \(W\):

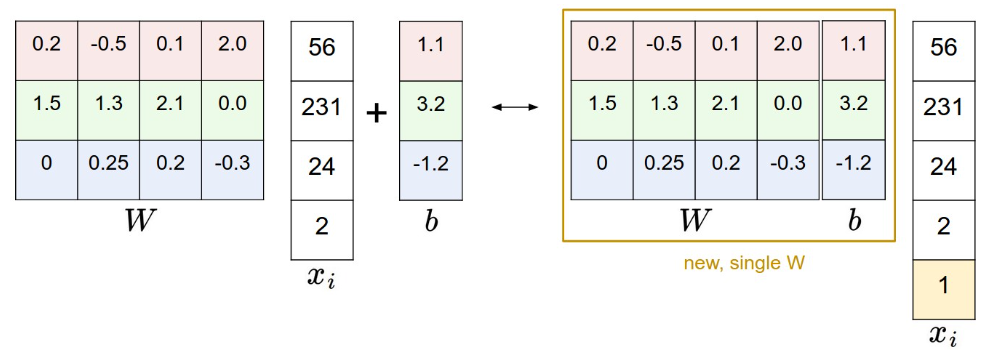
Preprocessing: center the data

For photos, pixel value: [0~255]

Now: [0…255] \(\Rightarrow\) [-127 .. 127] \(\Rightarrow\) [-1,1]

Loss function

Multiclass Support Vector Machine loss

For image \(x_i\) with label \(y_i\). Score function is \(f(x_i,W)\). Let \(s_j = f(x_i,W)_j\). Multiclass SVM loss: \[ L_i = \sum_{j\neq y_i}max(0,s_j-s_{y_i}+\Delta) \]

Regularization

\[ R(W) = \sum_k\sum_l W_{k,l}^2\\ L=\frac{1}{N}\sum_i L_i + \lambda R(W) \]

Or \[ L=\frac{1}{N}\sum_i\sum_{j\neq y_i}[max(0,f(x_i,W))_j-f(x_i,W)_{y_i}+\Delta]+\lambda \sum_k\sum_lW_{k,l}^2 \]

Softmax classifier

With \(f(x_i,W)=Wx_i\) unchanged, but for the loss: \[ L_i=-log(\frac{e^{f_{y_i}}}{\sum_je^{f_j}})\;or\;L_i=-f_{y_i}+log\sum_je^{f_j} \]

Optimization: Stochastic Gradient Descent

Visualizing the loss function

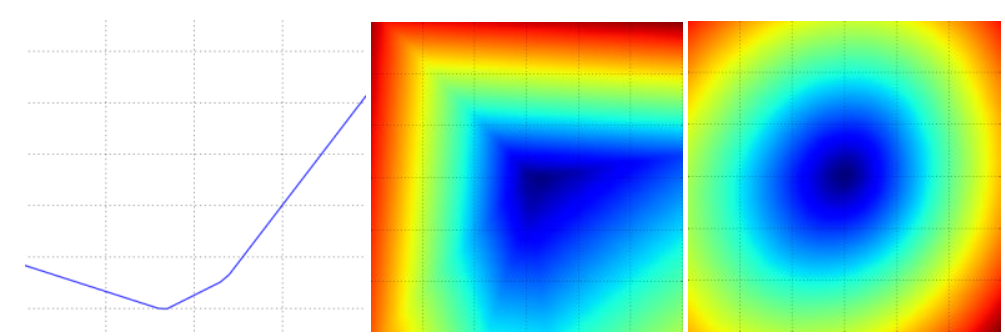
Optimization

Random search
Random local search
Following the gradient

\[ \frac{df(x)}{dx}=\lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h} \]

Use this definition to calculate grad of all dims

def eval_numerical_gradient(f, x):
  """
  a naive implementation of numerical gradient of f at x
  - f should be a function that takes a single argument
  - x is the point (numpy array) to evaluate the gradient at
  """

  fx = f(x) # evaluate function value at original point
  grad = np.zeros(x.shape)
  h = 0.00001

  # iterate over all indexes in x
  it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
  while not it.finished:

    # evaluate function at x+h
    ix = it.multi_index
    old_value = x[ix]
    x[ix] = old_value + h # increment by h
    fxh = f(x) # evalute f(x + h)
    x[ix] = old_value # restore to previous value (very important!)

    # compute the partial derivative
    grad[ix] = (fxh - fx) / h # the slope
    it.iternext() # step to next dimension

  return grad

In fact, we usually use \[ \frac{f(x+h)-f(x-h)}{2h} \] But this method of calculation is expensive and not so accurate. So maybe we can do it in a more “math” way.

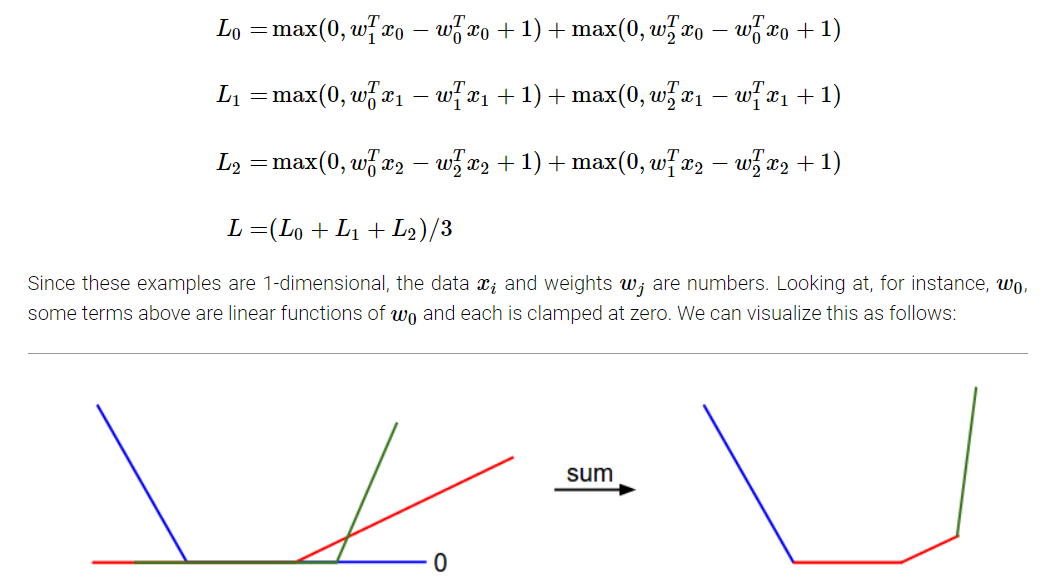
Take loss function of SVM as an example: \[ L_i = \sum_{j\neq y_i}[max(0,w_j^Tx_i-w_{y_i}^Tx_i+\Delta)] \] We can differentiate the function: \[ \Delta_{w_{y_i}}L_i = -(\sum_{j\neq y_i}1_{\{w_j^Tx_i-w_{y_i}^Tx_i+\Delta >0\}}) \\ \Delta_{w_{j}}L_i = 1_{\{w_j^Tx_i-w_{y_i}^Tx_i+\Delta >0\}}x_i \] With grad, we can do Gradient Descent by choosing a suitable step size(or learning rate),

1
2
3

while True:
  weights_grad = evaluate_gradient(loss_fun, data, weights)
  weights += - step_size * weights_grad # perform parameter update

However, if the dataset is very big, this can be extremely expensive. So we introduce Mini-batch gradient descent. That means we can only evaluate on a small subset to get a gradient.

The extreme case of this method is the subset has only one image. This process is called Stochastic Gradient Descent(SGD)

Backpropagation, Intuitions

Make good use of chain rule

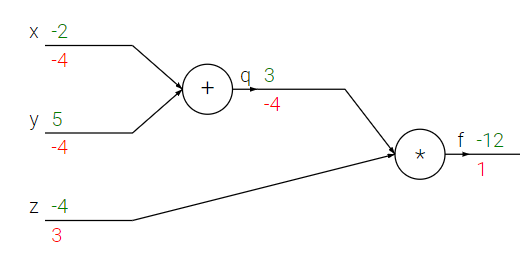
Add gate
Max gate
Multiply gate

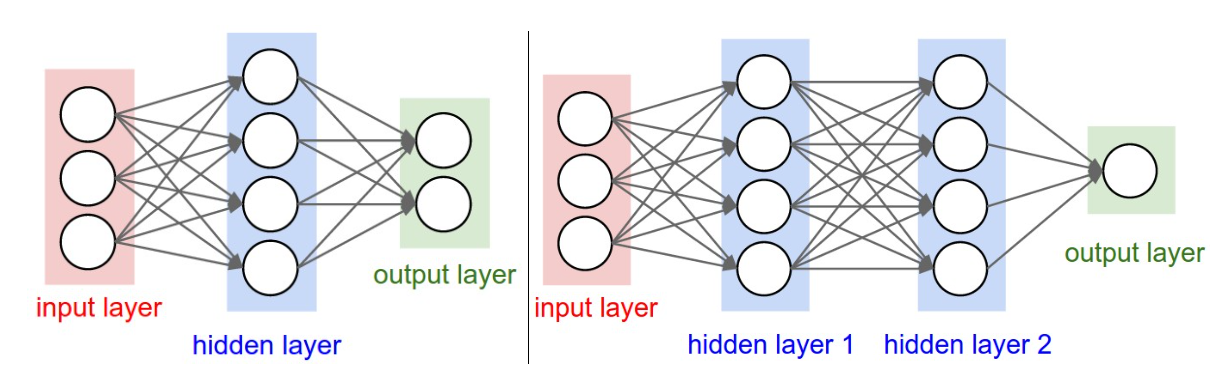
Neural Networks Part 1: Setting up the Architecture

input\(\rightarrow\)input\(\cdot\)weight\(\rightarrow\)input\(\cdot\)weight+bias\(\rightarrow\)activate-f(input\(\cdot\)weight+bias)

Ex \[ s=W_2max(0,W_1x)\\ s=W_3max(0,W_2max(0,W_1x)) \]

Single neuron as a linear classifier

Binary Softmax classifier
Binary SVM classifier
Regularization interpretation

Commonly used activation functions

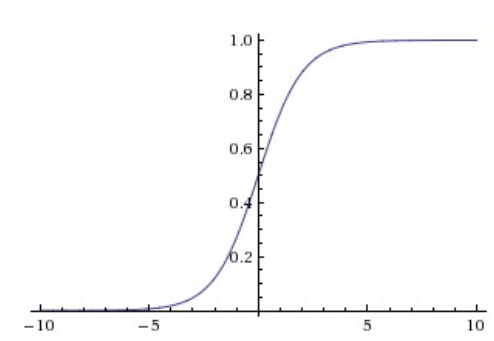
Sigmoid

\[ \sigma(x)=\frac{1}{1+e^{-x}} \]

Shortcomings:

1. kill gradients

2. not zero-centered

Tanh

\[ tanh(x)=2\sigma(2x)-1 \]

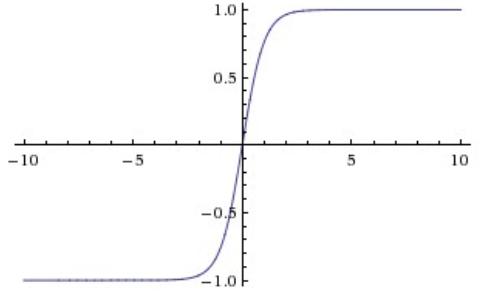
Solve the problem of not zero-centered

ReLU

\[ f(x)=max(0,x) \]

Advantages: greatly accelerate the convergence of stochastic descent; not so expensive as tanh/sigmoid

Shortcoming: may die when a large gradient flow through a ReLU neuron. May solved by setting a proper learning rate

Leaky ReLU

\[ f(x)=1_{(x<0)}(\alpha x)+1_{(x>=0)}(x) \]

in which \(\alpha\) is very small like 0.01

Maxout

\[ max(w_1^Tx+b_1,w_2^Tx+b_2) \]

Naming conventions When we talk about N-layer neural network, the input layer is not included in “N”.

Output Layer Unlike other layers, the output layer neurons most commonly do not have an activation function. (while the output layer is used to present scores of every class, it’s easy to understand)

Sizing neural networks Measure the size of neural: number of neurons/number of parameters

Representational power

Surveys has proven that given any continuous function f(x)and some ϵ>0, there exists a Neural Network g(x) with one hidden layer (with a reasonable choice of non-linearity, e.g. sigmoid) such that ∀x,∣f(x)−g(x)∣<ϵ. In other words, the neural network can approximate any continuous function.

Practically, deeper networks can work better than a single-hidden-layer network

For neural network, usually 3-layer networks will be better than 2-layer nets. But more deeper(4,5,6-layer) network rarely helps much more. But for convolutional network , it is different. Depth is a very important factor.

Regularization is very important, which can elite overfitting.

Neural Networks Part 2: Setting up the Data and the Loss

Data Preprocessing

Mean subtraction

code: X-=np.mean(X, axis = 0)

Normalization

code: X/=np.std(X, axis = 0)

PCA and Whitening

1
2
3

# Assume input data matrix X of size [N x D]
X -= np.mean(X, axis = 0) # zero-center the data (important)
cov = np.dot(X.T, X) / X.shape[0] # get the data covariance matrix

compute the SVD factorization of the data covariance matrix:

1	`U,S,V = np.linalg.svd(cov)`

where the columns of U are the eigenvectors and S is a 1-D array of the singular values. To decorrelate the data, we project the original (but zero-centered) data into the eigenbasis:

1	`Xrot = np.dot(X, U)`

dimensionality reduction:

1	`Xrot_reduced = np.dot(X, U[:,:100]) # Xrot_reduced becomes [N x 100]`

For whitening:

1
2
3

# whiten the data:
# divide by the eigenvalues (which are square roots of the singular values)
Xwhite = Xrot / np.sqrt(S + 1e-5)

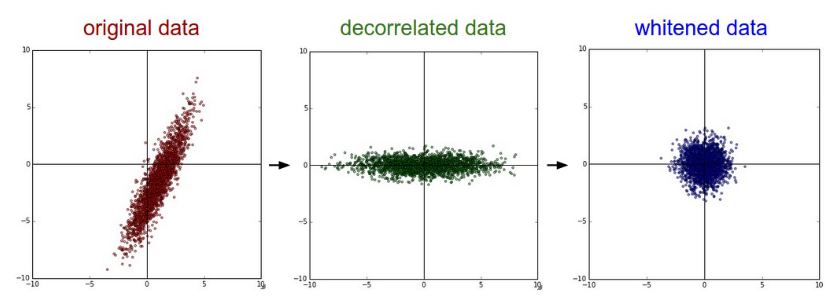
Common pitfall The mean must be computed only over the training data and then subtracted equally from all splits (train/val/test).

Weight Initialization

Pitfall: all zero initialization That will make every neuron do same thing.

Small random numbers aim: symmetry breaking. W=0.01*np.random.randn(D, H)

Calibrating the variances with 1/sqrt(n) W=np.random.randn(n) / sqrt(n) where n is the number of its inputs

Other: Sparse initialization, Initializing the biases(0), Batch Normalization

Regularization

L2 regularization May the most common. for all \(w\), add \(\frac{1}{2}\lambda w^2\) to the objective.

L1 regularization for each weight \(w\), we add the term \(\lambda |w|\) to the objective.

We can also combine the L1 regularization with the L2 regularization: \(\lambda _1|w|+\lambda_2w^2\), which is called Elastic net regularization.

Max norm constraints Enforce an absolute upper bound on the magnitude of the weight vector.

Dropout keep a neuron active with some probability \(p\) or setting it to zero otherwise

And there are many other methods about regularization. Bias regularization, per-layer regularization…

Loss functions

Let \(f=f(x_i;W)\) to be the activations of the output layer in a Neural Network.

Classification

SVM: \[ L_i=\sum_{j\neq y_i}max(0,f_j-f_{y_i}+1) \]

sometimes use \(max(0,(f_j-f_{y_i}+1)^2)\)

Softmax: \[ L_i=-log(\frac{e^{f_{y_i}}}{\sum_je^{f_j}}) \] Problem: Large number of classes When the set of labels is very large, Softmax becomes very expensive. It may be helpful to use Hierarchical Softmax.

Attribute classification

Both losses above assume that there is a single correct answer \(y_i\). But what if \(y_i\) is a binary vector where every example may or may not have a certain attribute \[ L_i=\sum_jmax(0,1-y_{ij}f_j) \] where \(y_{ij}\) is either +1 or -1

Neural Networks Part 3: Learning and Evaluation

Talking about learning process.

Gradient Checks

\[ \frac{df(x)}{dx}=\frac{f(x+h)-f(x-h)}{2h} \]

In order to compare the numerical gradient \(f_n'\) and analytic gradient \(f_a'\), we can use relative error: \[ \frac{|f_a'-f_b'|}{max(|f_a'|,|f_n'|)} \] In practive:

relative error >\(1e-2\): probably wrong
1e-2>relative error>1e-4: uncomfortable…
1e-4>relative error: OK…but without kinks(e.g. tanh and softmax), to high.
1e-7>relative error: happy

should use double precision

if jump kinks, may not be exact

In order to avoid above problems:

Use only few datapoints
be careful with h

Don’t let the regularization overwhelm the data
Remember to turn off dropout/augmentations

Before learning: sanity checks Tips/Tricks

Trace loss function

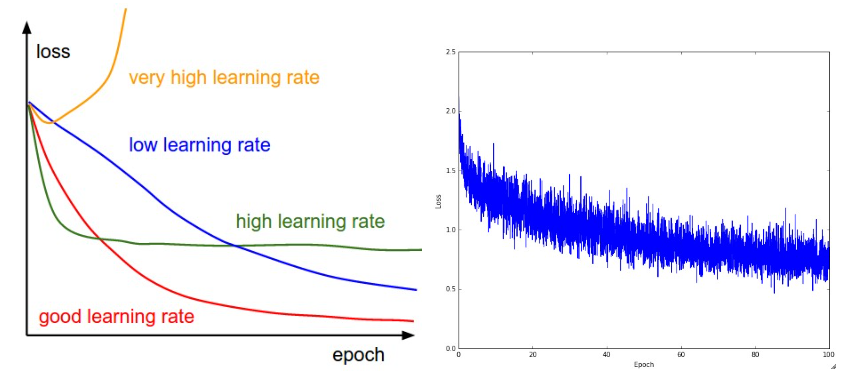
The right picture may mean the data is so small

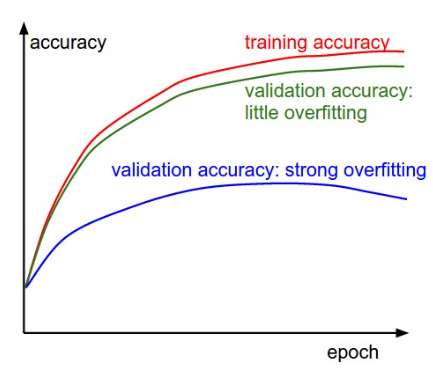
Trace train/val accuracy

Ratio of weights: updates

# assume parameter vector W and its gradient vector dW
param_scale = np.linalg.norm(W.ravel())
update = -learning_rate*dW # simple SGD update
update_scale = np.linalg.norm(update.ravel())
W += update # the actual update
print update_scale / param_scale # want ~1e-3

Activation / Gradient distributions per layer
First-layer Visualizations

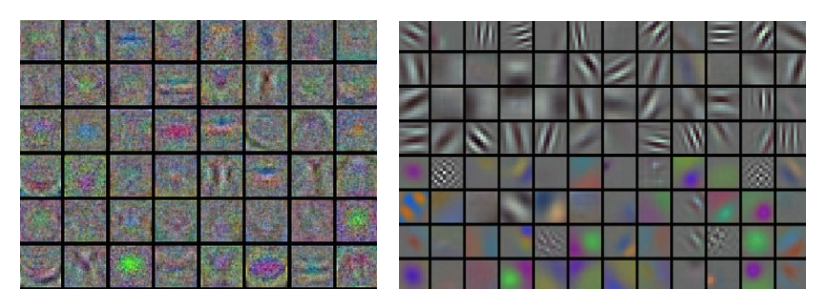
Left: many noise. may in trouble. Right: Nice, smooth

Parameter updates

First-order(SGD), momentum, Nesterov momentum

Vanilla update

1	`x += - learning_rate * dx`

Momentum update

1
2
3

# Momentum update
v = mu * v - learning_rate * dx # integrate velocity
x += v # integrate position

mu can be seen as the coefficient of friction in physics. (typical 0.9)

Nesterov Momentum

x_ahead = x + mu * v
# evaluate dx_ahead (the gradient at x_ahead instead of at x)
v = mu * v - learning_rate * dx_ahead
x += v

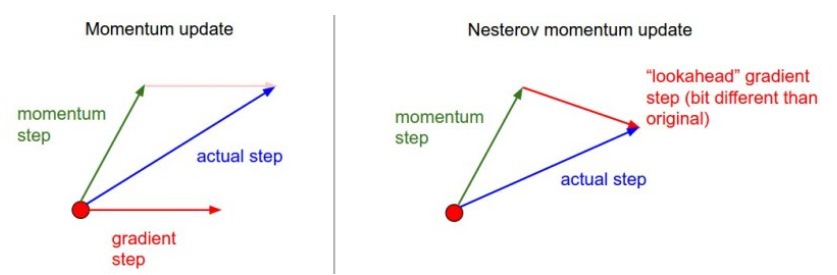
In practice, people like to rename \(x\_head\) as \(x\) :

1
2
3

v_prev = v # back this up
v = mu * v - learning_rate * dx # velocity update stays the same
x += -mu * v_prev + (1 + mu) * v # position update changes form

Annealing the learning rate

If the learning rate is too high, the system contains too much kinetic energy, unable to settle down into deeper, but narrower parts of the loss function.

Normally, there are three methods to decay the learning rate:

Step decay Reduce the learning rate every few epochs.
Exponential decay In math: \(\alpha = \alpha_0e^{-kt}\) in which \(\alpha_0,k\) are hyperparameters and \(t\) is the iteration number.
1/t decay In math: \(\alpha = \alpha _0/(1+kt)\) in which \(\alpha_0,k\) are hyperparameters and \(t\) is the iteration number

In practice, we find that the step decay is slightly preferable because the hyperparameters it involves

Second order methods

Basing on Newton’s method: \[ x\leftarrow x-[Hf(x)]^{-1}\nabla f(x) \] Multiplying by the inverse Hessian leads the optimization to take more aggressive steps in directions of shallow curvature and shorter steps in directions of steep curvature

However, because of the expensive cost of calculating the Hessian matrix, this method is impractical.

Per-parameter adaptive learning rate methods

Adagrad is an adaptive learning rate method originally proposed by Duchi et al.

1
2
3

# Assume the gradient dx and parameter vector x
cache += dx**2
x += - learning_rate * dx / (np.sqrt(cache) + eps)

eps: 1e-4~1e-8

shortcoming: the monotonic learning rate usually proves too aggressive and stops learning too early

RMSprop slide 29 of Lecture 6 of Geoff Hinton’s Coursera class: reduce Adagrad’s aggressive

1 2	`cache = decay_rate * cache + (1 - decay_rate) * dx*2 x += - learning_rate dx / (np.sqrt(cache) + eps)`

in which decay_rate is a hyperparameter: 0.9, 0.99, 0.999

Adam a recently proposed update looks a bit like RMSprop with momentum

simplified:

1
2
3

m = beta1*m + (1-beta1)*dx
v = beta2*v + (1-beta2)*(dx**2)
x += - learning_rate * m / (np.sqrt(v) + eps)

recommend: eps = 1e-8, beta1 = 0.9, beta2 = 0.999

With the bias correction mechanism, the update looks as follows:

# t is your iteration counter going from 1 to infinity
m = beta1*m + (1-beta1)*dx
mt = m / (1-beta1**t)
v = beta2*v + (1-beta2)*(dx**2)
vt = v / (1-beta2**t)
x += - learning_rate * mt / (np.sqrt(vt) + eps)

Hyperparameter optimization

The most common hyperparameters in context of Neural Networks include:

the initial learning rate
learning rate decay schedule(such as the decay constant)
regularization strength(L2 penalty, dropout strength)

Implementation make a worker and master

Prefer one validation fold to cross-validation a single validation set of respectable size substantially simplifies the code base, without the need for cross-validation with multiple folds

Hyperparameter ranges learning_rate = 10 ** uniform(-6, 1)

Prefer random search to grid search can be easily understand through following image:

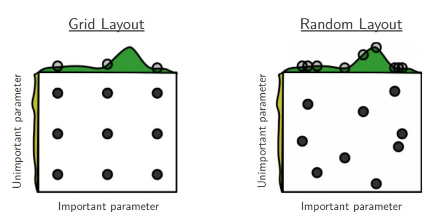
Careful with best values on border if we find that the results is on the border, we may set a bad range and miss the true best result.

Stage your search from coarse to fine

Bayesian Hyperparameter Optimization Spearmint, SMAC, and Hyperopt. However, in practical settings with ConvNets it is still relatively difficult to beat random search in a carefully-chosen intervals.

Evaluation

Model Ensembles

A reliable way to improve the performance of Neural Networks by a few percent: train multiple independent models, and at test time average their predictions.

The number of models \(\uparrow\) performance \(\uparrow\) the variety of models \(\uparrow\) performance \(\uparrow\)

Some approaches to forming an ensemble

Same model, different initializations

Use cross-validation to determine the best hyperparameters, then train multiple models with the best set of hyperparameters but with different random initialization.

shortcoming: variety is only due to iitialization

Top models discovered during cross-validation

Use cross-validation to determine the best hyperparameters, then pick the top few (e.g. 10) models to form the ensemble.

shortcoming: may include suboptimal models

Different checkpoints of a single model

Taking different checkpoints of a single network over time is training is very expensive

shortcoming: lack of variety

advantage: very cheap

Running average of parameters during training

Shortcoming of model ensembles: take longer to evaluate on test example.

A good idea: “distill” a good ensemble back to a single model by incorporating the ensemble log likelihoods into a modified objective.

Convolutional Neural Networks

Convolutional Neural Networks: Architectures, Convolution / Pooling Layers

CNN base on an assumption that the inputs are images.

Layers used to build ConvNets

Convolutional Layer, Pooling Layer, Fully-Connected Layer

Convolutional Layer

filter with size like \(5\times 5\times 3\)

During the forward pass, we slide (more precisely, convolve) each filter across the width and height of the input volume and compute dot products between the entries of the filter and the input at any position

\(\rightarrow\) produce a separate 2-dimensional activation map

The spatial extent of this connectivity: a hyperparameter called the receptive field

Depth, Stride, Zero-padding

Depth: depend on the number of filter. Called “deep column” or “fiber”

Stride: the number of pixel the filter will move when we slide it

Zero-padding: pad the input volume with zeros around the border

In math. the input volume size :\(W\), the receptive size of the Conv Layer neurons: \(F\), the stride with which they are applied: \(S\), the amount of zero padding used: \(P\)

then the output: \((W-F+2P)/S+1\)

Summary

Accept size: \(W_1\times H_1\times D_1\)
Require:
- number of filters \(K\)
- spatial extent \(F\)
- stride \(S\)
- the amount of zero padding \(P\)
Produce size: \(W_2 \times H_2 \times D_2\)
- \(W_2=(W_1-F+2P)/S+1\)
- \(H_2=(H_1-F+2P)/S+1\)
- \(D_2=K\)

common set: \(F=3, S=1, P=1\)

Backpropagation The backward pass for a convolution operation (for both the data and the weights) is also a convolution (but with spatially-flipped filters).

\(1\times 1\) convolution note that we have 3 channels. so it’s not meaningless

Dilated convolutions have filters that have spaces between each cell, called dilation.

##### Pooling layer

Common: Max

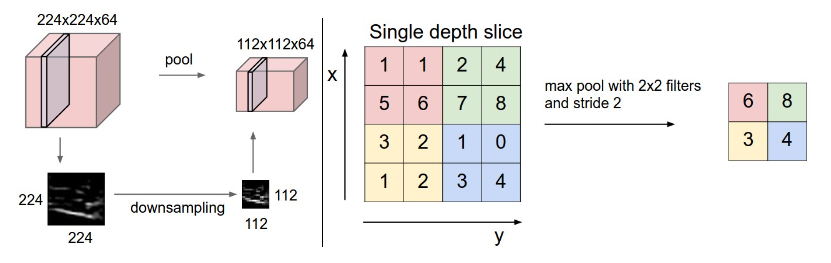
Accept size \(W_1\times H_1\times D_1\)
Hyperparameters
- spatial extent \(F\)
- stride \(S\)
Produce size \(W_2\times H_2\times D_2\)
- \(W_2=(W_1-F)/S+1\)
- \(H_2=(H_1-F)/S+1\)
- \(D_2=D_1\)

Common: \(F=3, S=2\) more commonly \(F=2, S=2\)

Normalization Layer

These layers have since fallen out of favor because in practice their contribution has been shown to be minimal, if any. For various types of normalizations, see the discussion in Alex Krizhevsky’s cuda-convnet library API.

Fully-connected layer

Just like Neural Network section

Converting Fully Connected layers to CONV layers

Each of these conversions could in practice involve manipulating (e.g. reshaping) the weight matrix \(W\) in each FC layer into CONV layer filters. It turns out that this conversion allows us to “slide” the original ConvNet very efficiently across many spatial positions in a larger image, in a single forward pass.

ConvNet Architectures

The most common pattern:

1	`INPUT -> [[CONV -> RELU]N -> POOL?]M -> [FC -> RELU]*K -> FC`

N >= 0 (and usually N <= 3), M >= 0, K >= 0 (and usually K < 3).

INPUT -> FC, implements a linear classifier.
INPUT -> CONV -> RELU -> FC
INPUT -> [CONV -> RELU -> POOL]*2 -> FC -> RELU -> FC. Here we see that there is a single CONV layer between every POOL layer.
INPUT -> [CONV -> RELU -> CONV -> RELU -> POOL]*3 -> [FC -> RELU]*2 -> FC Here we see two CONV layers stacked before every POOL layer.

Prefer a stack of small filter CONV to one large receptive field CONV layer.

Layer Sizing Patterns

Input Layer

Should be divisible by 2 many times.

Ex. 32 (e.g. CIFAR-10), 64, 96 (e.g. STL-10), or 224 (e.g. common ImageNet ConvNets), 384, and 512.

Conv Layer

3x3 or 5x5 Step \(S=1\), zero

Pool Layer

2x2 , stride = 2(sometimes 3x3, stride = 2)

Use stride of 1 in CONV:

Smaller strides work better in practice.
Allows us to leave all spatial down-sampling to the POOL layers, with the CONV layers only transforming the input volume depth-wise.

Use padding:

If the CONV layers were to not zero-pad the inputs and only perform valid convolutions, then the size of the volumes would reduce by a small amount after each CONV, and the information at the borders would be “washed away” too quickly.

Compromising based on memory constrains:

people prefer to make the compromise at only the first CONV layer of the network. For example, one compromise might be to use a first CONV layer with filter sizes of 7x7 and stride of 2 (as seen in a ZF net). As another example, an AlexNet uses filter sizes of 11x11 and stride of 4.

Case Studies

LeNet
AlexNet
ZF Net
GoogleNet
VGGNet
ResNet

VGG:

INPUT: [224x224x3]        memory:  224*224*3=150K   weights: 0
CONV3-64: [224x224x64]  memory:  224*224*64=3.2M   weights: (3*3*3)*64 = 1,728
CONV3-64: [224x224x64]  memory:  224*224*64=3.2M   weights: (3*3*64)*64 = 36,864
POOL2: [112x112x64]  memory:  112*112*64=800K   weights: 0
CONV3-128: [112x112x128]  memory:  112*112*128=1.6M   weights: (3*3*64)*128 = 73,728
CONV3-128: [112x112x128]  memory:  112*112*128=1.6M   weights: (3*3*128)*128 = 147,456
POOL2: [56x56x128]  memory:  56*56*128=400K   weights: 0
CONV3-256: [56x56x256]  memory:  56*56*256=800K   weights: (3*3*128)*256 = 294,912
CONV3-256: [56x56x256]  memory:  56*56*256=800K   weights: (3*3*256)*256 = 589,824
CONV3-256: [56x56x256]  memory:  56*56*256=800K   weights: (3*3*256)*256 = 589,824
POOL2: [28x28x256]  memory:  28*28*256=200K   weights: 0
CONV3-512: [28x28x512]  memory:  28*28*512=400K   weights: (3*3*256)*512 = 1,179,648
CONV3-512: [28x28x512]  memory:  28*28*512=400K   weights: (3*3*512)*512 = 2,359,296
CONV3-512: [28x28x512]  memory:  28*28*512=400K   weights: (3*3*512)*512 = 2,359,296
POOL2: [14x14x512]  memory:  14*14*512=100K   weights: 0
CONV3-512: [14x14x512]  memory:  14*14*512=100K   weights: (3*3*512)*512 = 2,359,296
CONV3-512: [14x14x512]  memory:  14*14*512=100K   weights: (3*3*512)*512 = 2,359,296
CONV3-512: [14x14x512]  memory:  14*14*512=100K   weights: (3*3*512)*512 = 2,359,296
POOL2: [7x7x512]  memory:  7*7*512=25K  weights: 0
FC: [1x1x4096]  memory:  4096  weights: 7*7*512*4096 = 102,760,448
FC: [1x1x4096]  memory:  4096  weights: 4096*4096 = 16,777,216
FC: [1x1x1000]  memory:  1000 weights: 4096*1000 = 4,096,000

TOTAL memory: 24M * 4 bytes ~= 93MB / image (only forward! ~*2 for bwd)
TOTAL params: 138M parameters

Computational Considerations

There are three major sources of memory to keep track of:

From the intermediate volume sizes
From the parameter sizes
Every ConvNet implementation has to maintain miscellaneous memory, such as the image data batches, perhaps their augmented versions, etc.